5.4 Angular Momentum and Its Conservation
3 min read•january 30, 2023
Daniella Garcia-Loos
Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
Conservation of Angular Momentum
Conservation of Angular Momentum: Angular momentum of a system is conserved unless there is an outside torque acting on the system.
Angular momentum is a measure of an object's rotation around an axis, and is given by the product of the object's moment of inertia and its angular velocity.
- The total angular momentum of a system of objects is the sum of the angular momenta of the individual objects.
- In an isolated system, the total angular momentum is conserved, meaning that it remains constant over time.
- This means that if an external torque is applied to an object, causing its angular velocity to change, the angular momentum will remain constant, provided that no external torques are acting on the object.
- Similarly, if an external torque is applied to an object, causing its moment of inertia to change, the angular velocity will change such that the angular momentum remains constant.
- Conservation of angular momentum is used to explain phenomena such as the stability of planets and stars, the precession of a spinning top, and the behavior of spinning objects in the presence of external forces.
- Conservation of angular momentum can be applied to both rigid bodies and non-rigid bodies, as long as the body remains in a rigid state and the external torques acting on the body are not too large.
Which means that torque is the slope of an angular momentum vs. time graph!
⚠️ Common misconception: You cannot just multiply r by translational momentum to change it to angular!! L does not equal mvr for anything other than a point/particle!
Common Situations of Conservation of Angular Momentum
Disks Colliding:
This situation is extremely similar to pool ball scenarios we've seen in the past with linear momentum, however, we typically considered those pool balls as a particle/point in space. Disks have some rotational inertia so they can apply torque on each other. However, it is important to remember that angular momentum is conserved because these torques are inside the system!
Here's an example of a disk collision below:
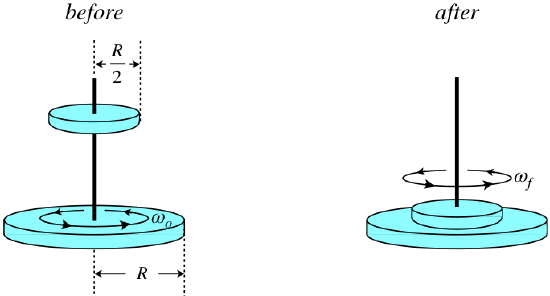
Taken from LibreTexts
Ballistic Pendulum:
A ballistic pendulum is a device used to measure the speed of a projectile, such as a bullet. To solve a ballistic pendulum problem, you will need to know the initial speed of the projectile and the mass of the pendulum. You can then use the conservation of energy and the conservation of momentum to calculate the final speed of the projectile and the maximum height of the pendulum's swing. Here are the steps to solve a ballistic pendulum problem:
- Identify the initial and final states of the system. In this case, the initial state is the bullet moving with a certain velocity and the pendulum at rest, while the final state is the bullet embedded in the pendulum, which is swinging at some height.
- Use the conservation of energy to find the maximum height of the pendulum's swing. The initial kinetic energy of the bullet is equal to the final gravitational potential energy of the pendulum.
- Use the conservation of momentum to find the final velocity of the bullet. The initial momentum of the bullet is equal to the final momentum of the bullet and pendulum combined.
- Once you have the final velocity and the mass of the pendulum, you can use the equation for kinetic energy to find the speed of the bullet.
- Remember that the final velocity of the bullet is very small compare to the initial velocity, and assuming the pendulum is much heavier than the bullet, to get a more accurate result you can use the conservation of energy and momentum equations for a system of two masses (bullet+pendulum)
You can see an example of the scenario below:
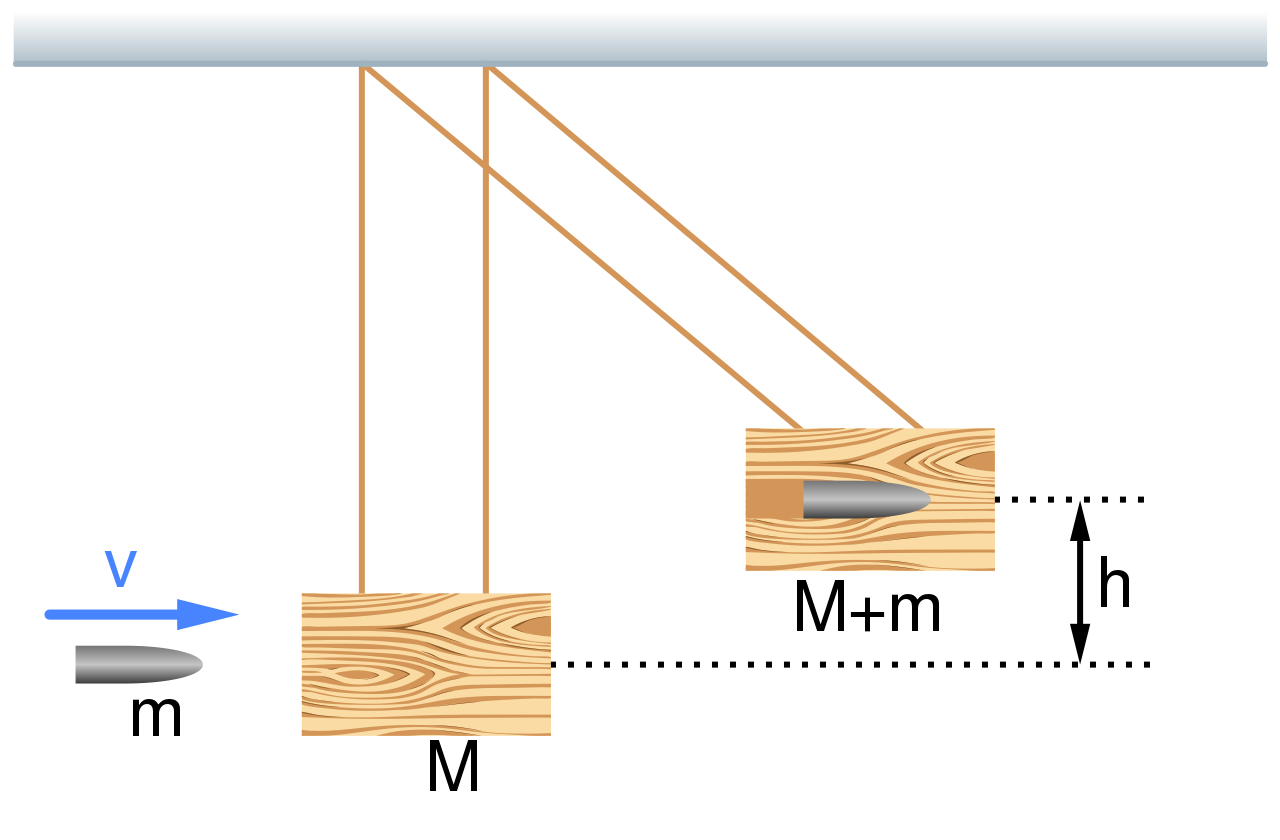
Taken from Wikimedia Commons
Typically it can be solved with a combination of conservation of energy and momentum! When the pendulum has some rotational inertia, we have to use conservation angular momentum for the bullet-pendulum system.
Satellites:
We'll cover this situation in Unit 7, but just know it exists!
Practice Questions:
1)

Answer:
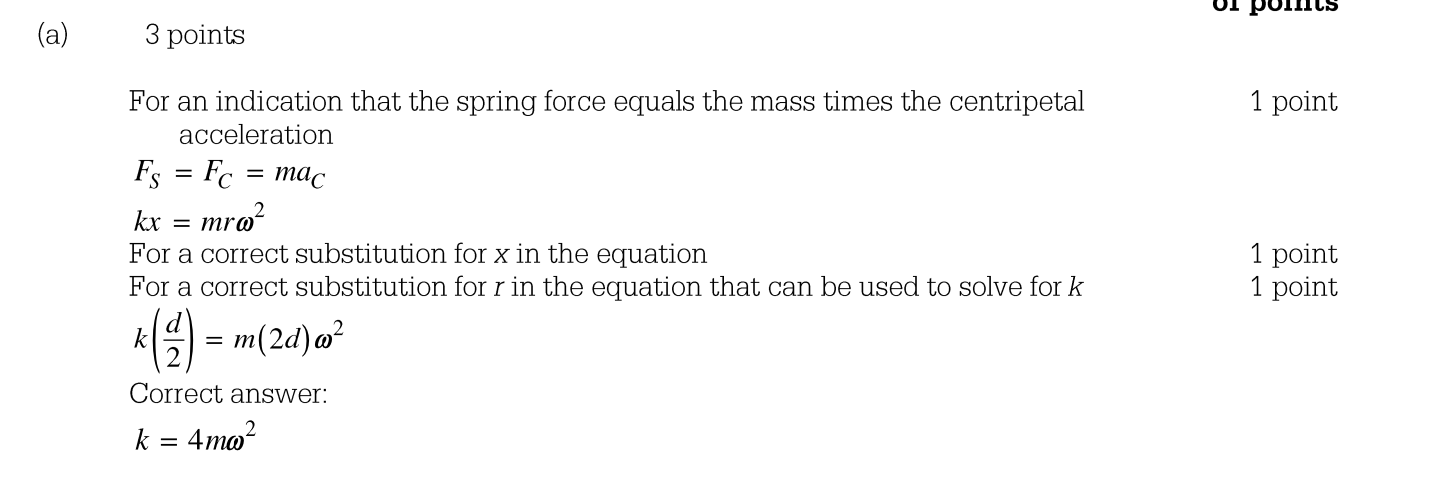
2)

Answer:

3)
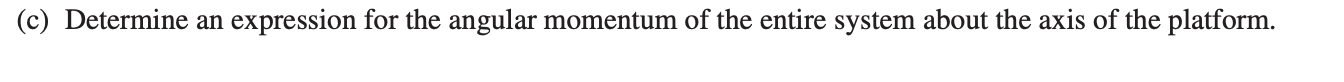
Answer:

4)

Answer:

Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
🙏Exam Reviews

© 2023 Fiveable Inc. All rights reserved.