SAT Math: Proportional Reasoning & Relationships 📈
5 min read•august 25, 2021
SAT 🎓
62 resourcesSee Units
Overview of the SAT Math Section
How long is the SAT Math section?
The Math section of the SAT will be the third and fourth sections and will look like the following:
- one 25-minute section completed without the use of a calculator (of any kind, no exception), followed by
- one 55-minute section that allows the use of a graphing calculator, even though the technology is not always necessary.
SAT Math Topics
These questions (both with-calculator and no-calculator) test on four major content areas: the Heart of Algebra, Problem Solving, Data Analysis, and the Passport to Advanced Math.
- Each section of the Math portion of the SAT begins with multiple-choice questions, each with four choices.
- Following the multiple-choice questions will be questions that do not have choices. Instead, students will bubble in their answers; these questions are often called "grid-in" questions.
- The reference sheet will be available for ALL Math sections of the SAT, regardless of whether calculators are allowed on that section or not.
Breakdown of the Two SAT Math Sections
| Section | Number of Questions | Time ⏱ |
| No Calculator | 15 multiple-choice, 5 grid-ins | 25 Minutes |
| Calculator | 30 multiple-choice, 8 grid-ins (including one Extended Thinking question) | 55 Minutes |
| Total | 58 Questions | 80 Minutes |
- On the calculator portion, some of the grid-ins will relate to one another as part of an Extended Thinking question.
Topics Related to “Proportional Reasoning & Relationships”
- Reading and adjusting for different units of measurement
- Percentage problems
- Change in percentages
- Read data from charts, graphs, or tables
- Determine whether data is linear or exponential
What You Need to Know
- Be able to change/convert to common units.
- A percentage is a part of 100
- Change in percentage is the difference in % divided by total * 100
- Interpret data from charts, graphs, or tables
- How to find and interpret line of best fit to given data
- If there is a common difference in data values, the relationship is linear
- If there is a common product between data, the relationship is exponential
SAT Math Sample Questions Explanations
Non-Calculator Practice Problems
General directions for this section that should be expected:
- The use of a calculator is not allowed at all in this section.
- All variables and expressions represent real numbers unless otherwise specified.
- Figures are drawn to scale unless otherwise specified.
- Assume that all figures lie in a plane.
- Assume that the domain of a given function is the set of all real numbers unless otherwise specified.
1. Let’s start with a medium-difficulty problem:
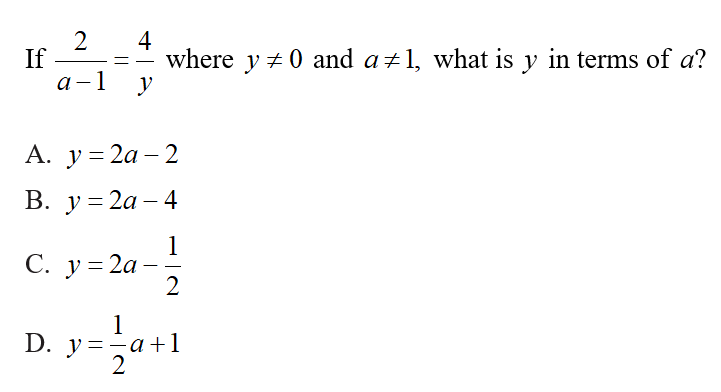
AP college board SAT practice problems
The correct answer is A:
Looking at the original problem, multiply both sides by the other denominator (get common denominators). This will simplify to 2y=4a-4. Solving for y will then give y=2a-2.
2. This example is considered medium difficulty:

AP college board SAT practice problems
The correct answer is B:
Simplify the numerators and then cross multiply, which will result in 45k+27=54+6k. Solving for k will give you 9/13.
3. This example is considered “hard” difficulty, with reading thrown in as well:

AP college board SAT practice problems
The correct answer is B:
⅕ is the part of the job that two printers can complete in one hour, and each part on the left is the part of the ⅕ that each machine does. Since one printer is twice as fast as the other, 2/x is the part of the job completed by the faster printer, and 1/x is the slow printer contribution.
Calculator section practice problems
General directions for this section you should expect to see:
- A graphing calculator is allowed for this section, although not often necessary. (use the calculator as a tool, not as a crutch!)
- All variables and expressions represent real numbers unless otherwise specified.
- Given pictures or figures are drawn to scale unless otherwise specified.
- Assume that all figures lie in a plane.
- Assume that the domain of a given function is the set of all real numbers unless otherwise specified.
1. The following question is considered easy in difficulty, but still requires reading and a solid understanding of the percent relationship.

AP college board SAT practice problems
The correct answer is B:
Aaron’s total stay will be the fixed-rate or $99.95 plus the tax, which is found by multiplying 0.08*99.95… this per x days, added to the one time charge of $5… combining, this will give (99.95 + 0.08*99.95)*x + 5, which simplifies to choice B.
2. The following sample question is considered medium difficulty:

AP college board SAT practice problems
The correct answer is B:
The number of gallons of gas used per hour is 50/21, or (50/21)*t hours.
Since the car’s gas tank has 17 gallons of gas at the start of the trip, and the resulting function will be the starting 17 minus the amount of gas used each hour, giving 17 - (50/21)*t.
3. The following example is considered “medium” in difficulty. Conversion between megabytes and gigabytes and converting between hours, minutes, and seconds is necessary for success on this problem.

AP college board SAT practice problems
The correct answer is B:
1 hour = 3600 seconds.
1 gigabit = 1024 megabits.
3*3600*11 = 118,800 megabits.
Dividing this by 1024 will give 118,800/1024=116.015625 gigabits each day.
If each image is 11.2 gigabits, then 116.0156/11.2=10.3585, which is approximately 10 images per day (round down).
4. This example is considered “hard” in difficulty. It is a proportional relationship, also probability. The key is to recall that information about a random sample can be extrapolated to estimate a population parameter.

AP college board SAT practice problems
The correct answer is 7212:
d/7500 = exchange rate for dollars to rupees.
Rupees to dollars = (d/7500)*r
Using Traveler card would cost 1.04*(d/7500)*r dollars
To figure out how many rupees need to be spent to make the Traveler card a better option, think:
1.04*(d/7500)*r ≥ d and solve for r…. 1.04r ≥ 7500, which gives r ≥ 7211.53846 → 7212.
Closing
Congratulations! You’ve made it to the end of SAT Math - Statistics and Data Analysis prep 🙌 You should have a better understanding of the Math sections for the SAT© , topic highlights, what you will have to be able to do in order to succeed, as well as have seen some practice questions that put the concepts in action. Good luck studying for the SAT Math section 👏
Need more resources? Check out our complete SAT Math Study Guide w/ Practice Problems. Pressed on time? Access our SAT cram sessions and watch the Night Before the SAT cram session. You got this 🥳.
More Helpful SAT Math Resources
Browse Study Guides By Unit
📚Reading
📝Writing and Language
✍️Essay
✏️Frequently Asked Questions

© 2023 Fiveable Inc. All rights reserved.